Having been born and raised in Minnesota, I’ve had a lot of time to think about the most efficient way to shovel snow. Being as it’s now the dead of winter, I thought I’d formalize my findings on the subject so far. If you are also a long-time resident of the snowy climates, these findings might be painfully obvious to you; but if you’re one of those who find themselves suddenly and inexplicably transplanted to a snowy state, you might find it very useful.

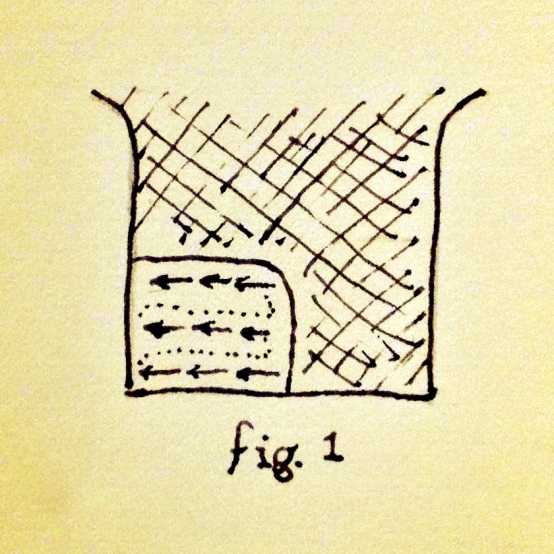
In fig. 1 we see a common shoveling pattern. The shoveler begins in the center of the driveway on the end nearest the house (bottom of diagram) and starts shoveling outward, reaching the edge of the drive in three strokes (arrows in diagram). He or she then walks back to the middle of the driveway (dotted line) and repeats the proceedure.

This is a pretty shabby way to shovel, because you end up walking over the whole driveway twice: you walk over each area once to shovel it, and once while retracing your steps to start the next row.

With a little math, we can see precisely why this method is not optimal, and compare it to other possible methods. Let’s call $L$ the length of the driveway, $W$ the width, and (for simplicity) use $s$ as our unit of measure, equal to the width of your shovel. So the total distance you would travel when shoveling using the above method is $2(LW)$, which on a driveway measuring $30s \times 6s$ means you will walk $360s$ — quite a lot of wasted distance when you consider the area of the driveway only contains $180s$ of distance to begin with.

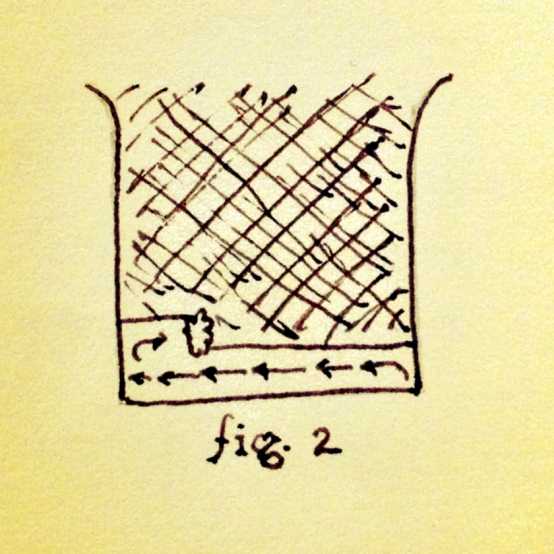
A first attempt at an improvement might have you start in one of the corners, shovel in one direction to the edge of the driveway, then turn around and shovel in the other direction (fig. 2). This would be an optimal pattern for plowing a field, since the distance covered is exactly $LW$. In practice, however, this is often impractical for snow shoveling. In the first couple of strokes, you would have to throw the snow nearly the entire length of the row ($W$) in order to clear it from the driveway. This is wasted effort, since none of the snow is more than $\frac{1}{2}W$ from at least one edge of the drive. For this reason, this pattern is optimal only when there’s so little snow that can push your shovel from one edge of the driveway to the other and accumulate no more than a shovelfull of snow.

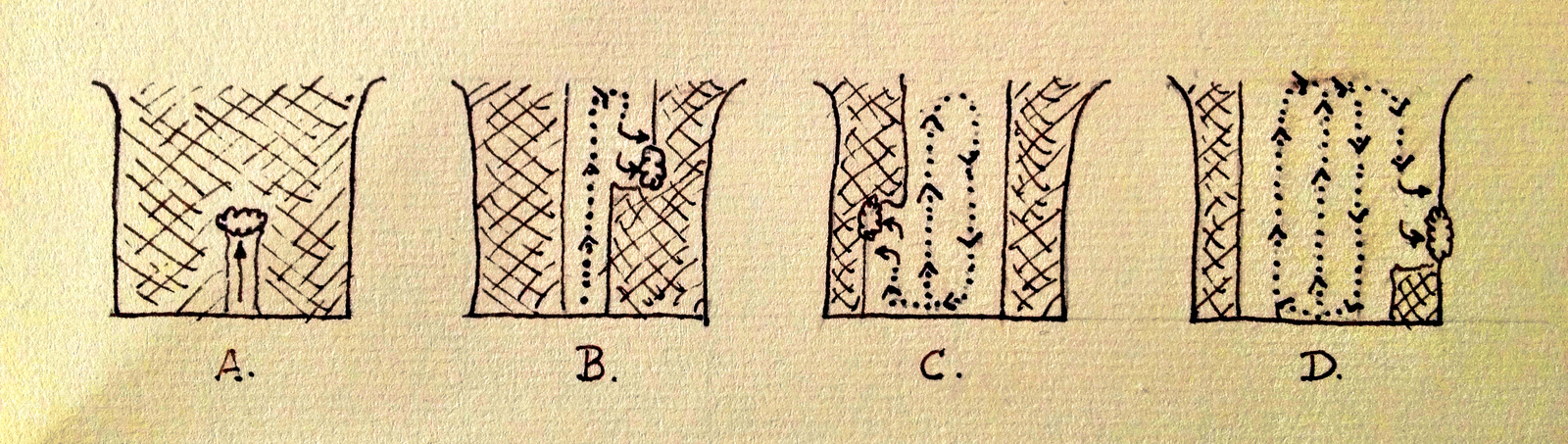
Figure 3 shows a pattern that is optimal for all non-trivial amounts of snowfall. You begin by clearing a path $1s$ wide down the center of the driveway (A). You then turn around and begin working back towards the other end of the driveway, clearing the next $1s$ column with single shovel strokes (B). At the end of this second column, you again walk across to the opposite edge of the cleared area and clear the next column (C) and so on, moving in a square that widens out from the middle until the driveway is cleared (D).

Using this method, there is very little wasted travel, and you never have to throw snow further than $\frac{1}{2}W$. The distance traveled is roughly $L \times W$ — plus only a little extra to walk across the end of the driveway once each column is finished. We can discover the precise amount of this extra travel as follows: at the end of the first column you must walk $1s$ horizontally to start the next column, and after the second column you must walk $2s$, and so on up to $(W - 1)s$:

$$1s + 2s + \dotsb + (W-1)s$$

(Note that we stop at $W-1$ since at the end of the final column the shoveling is considered complete.) The formula to find the sum of all numbers between 1 and a given number $N$ is $(N+1)\frac{N}{2}$ (see example in the footnotes¹). To find the sum of all numbers from $1$ to $W-1$ we use $(W\color{gray}{-1+1})\frac{W-1}{2}$, making the complete distance traveled equal to

$$LW + \left(W\frac{W - 1}{2}\right)s$$

In our example driveway where $L = 30s, W = 6s$, this works out to

$$(30s \times 6s) + 6\frac{5}{2}s = \color{red}{188\frac{1}{2}s}$$

which represents a vast improvement over the distance of $360s$ needed to finish the driveway using the original method.